Bayesian matches

The probabilistic argument used for simple matches, for belief concerning the true cause of a typed report, can be developed in a fully Bayesian framework.

In a Bayesian belief representation an observed match, “Match?” = 1, at a randomly chosen source depends on whether that source is the “True cause?” of the report. The conditional probability table for the observed match is conveniently written as

p(“Match?” | “True cause?”, nT) = Binomial(1, 1) if “True cause?” = 1 else Binomial(1, nT-1)

where the number of types, nT , determines the random matching probability. In the Bayesian representation the observed match, an observable, is explicit and the number of unobserved matches, i.e. m – 1, is implicit. Prior beliefs about the true cause depend only on the number of (equivalent) sources, NS, and a network representation again has four nodes. A domain model is shown below.

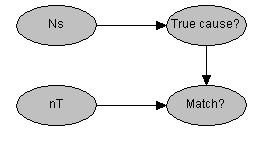
In this network it is plain that observing a match at a random source, out of 101 sources, changes belief about causality to above 71% when there are 250 distinct types. In some respects the explicit appearance of the observed match ensures that the fully Bayesian representation of events is more useful for biotracing applications.

---